To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `(xy^3y)dx2(x^2y^2xy^4)dy=0`23 Exercises (Linear Equations) Q1 Find the general solution of the given differential equation 1 3 dy y = (3x dx dy x 2y = 3 dx y' = 2y x2 5 Q2 Find the solution of the differential equation that satisfies the given initial conditionIt's so write it as M (x,y)dx N (x,y)dy =0 with M = 2x^3 y^3 , N = xy^2 ,M_y =3y^2 # N_x = y^2 , but (M_y N_x)/N =4/x depends only on x The integrating factor is 1/x^4 and the new equation is P (x,y)dx Q (x,y)dy =0 with P = 2/x y^3/x^4 , Q = y^2/x^3 and P_y = Q_x = 3y^2/x^4

Section 3 1 1 Implicitly Differentiate To Find Dy Dx Y3 X2 4 Slideshow And Powerpoint Viewer 2 Implicitly Differentiate To Find Dy Dx Y 4 X 3 2x 4y 3 Dy 3x 2 2 Dx Dy 4y
(x-y-2)dx-(2x-2y-3)dy=0
(x-y-2)dx-(2x-2y-3)dy=0- Attempt dy dx = y(x y3) x(y3 − x) Let y3 = xt Then 3y2dy dx = t xdt dx Therefore (t xdt dx) (3y2) = t(t 1) y2(t − 1) and hence xdt dx = 2t2 4t t − 1 Integrating, ln cx = 3 4ln t 2 − 1 4ln t Simplyfing, cx2 = y3 2x y but the given answer is y = cx1 / 3 Where have I made a mistake?Steps for Solving Linear Equation ( x ^ { 3 } y ^ { 2 } ) d x 3 x y ^ { 2 } d y = 0 ( x 3 y 2) d x − 3 x y 2 d y = 0 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3




التامة
Dx =sin5x 2 dx e3x dy =0 3 (x1) dy dx = x6 4 xy0 =4y 5 dy dx = y3 x2 6 dx dy = x2y2 1x 7 dy dx = e3x2y 8 ¡ 4y yx2 ¢ dy − ¡ 2xxy2 ¢ dx =0 9 2y(x1)dy = xdx 10 ylnx dx dy = µ y 1 x ¶ 2 (11) dy dx =sin5x, dy =sin5xdx, Z dy = Z sin5xdx, y = − 1 5 cos5xc, c ∈R (12) dxe3x dy =0 Solve (xy2)dx (x2y3) dy =0 Asked by Phani on Be the first to answer this Question ! Find an answer to your question (xy2)dx(x2y3)dy=0 solve this differential equations mohitparmar mohitparmar Math Secondary School answered • expert verified (xy2)dx(x2y3)dy=0 solve this differential equations 1 See answer mohitparmar is waiting for your help Add your answer and earn points
Question Q3/ Solve The Following Equations 1 X(2y 3)dx (x2 1)dy = 0 Dy 2 4y Dx X(y3) 3 Y' = 2xy /(x2 Y2) 4 Dy_ Xy Xy = Dx 5 (x23y2 X Y 2)dx (x 6xy Y2 10)dy = 0 This question hasn't been answered yet Ask an expertTheory Roots of a product 51 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves productThe equation M (x,y)dx N8x,y)dy = 0 with M = xy y^2 y N =x^2 3xy 2x is not exact because M_y = x 2y 1 # N_x = = 2x 3y 2 However (N_x M_y)/M = 1/y then IF = y A new equation follows P (x,y)dx Q (x,y)dy = 0 with P = xy^2 y^3 y^2 , Q = yx^2 3xy^2 2xy This
Click here👆to get an answer to your question ️ Solve x^2ydx = (x^3 y^3)dy = 0Use the distributive property to multiply x 2 y 3 d x d by y To find the opposite of x^ {2}dy^ {4}xdy, find the opposite of each term To find the opposite of x 2 d y 4 x d y, find the opposite of each term Combine ydx and xdy to get 2ydx Combine − y d x and − x d y to get − 2 y d x The solution of x^2y – x^3 (dy/dx) = y^4 cos x;



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero



How To Solve The Differential Equation 2y 3xy 2 Dx X 2x 2y Dy 0 Quora
Solve (xy2)dx(x2y3)dy=0 Maths Differential Equations NCERT Solutions;Solve (1 ) = x(y2 1) dx dy x Sol dx x x y x(2y3)dx(x21)dy=0 ans (x21)(2y3)=c 2 dy=exy dx ans ey=exc 3 sin x dx dy cosh 2y=0 ans sinh 2y2cosx=c 4 xeydy 0 2 1 = dx y x ans ey(y1) 2 x2 ln x=c 5 2 =1 dx dy xy ans y = x2 c 1 2 3 3 2 2 Homogeneous I'm at the beggining of a differential equations course, and I'm stuck solving this equation $$(x^2y^2)dx2xy\ dy=0$$ I'm asked to solve it using 2 different methods I proved I can find integrating factors of type $\mu_1(x)$ and $\mu_2(y/x)$If I'm not wrong, these two integrating factors are $$\mu_1(x)=x^{2} \ \ , \ \ \mu_2(y/x)=\left(1\frac{y^2}{x^2}\right)^{2}$$ Then, I've




Solve 3xy 2ay 2 Dx X 2 2axy Dy 0 Mathematics Stack Exchange




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12
dY dX d Y d X = X2Y ℓ2m−3 2XY 2ℓm−3 X 2 Y ℓ 2 m − 3 2 X Y 2 ℓ m − 3 = X2Y 2Xy X 2 Y 2 X y If l, m are chosen to satisfy ℓ ℓ 2m 3 = 0 2ℓ ℓ m 3 = 0 (where ℓ ℓ = 1 and m = 1) In X, Y the equation is homogeneous and of the first degree Put YCreate your account View this answer (x23y2) dx−2xy dy = 0 ( x 2 3 y 2) d x − 2 x y d y = 0 ⇒ dy dx = x23y2 2xy ⇒ d y d x = x 2 3 y 2 2 x y Substitute {eq}y=vx See full Solution for the Differential Equation (x y 2) dx (x 2y 3) dy = 0 Solve the differential equation (x y 2) dx (x 2y 3) dy = 0 Asked by Tejinder Samra on



Solve 2 Y 3 Xy Dy Dx 0 Given That Y 1 2 Studyrankersonline




Solve The De Y 3 6xy 4 Dx 3 Xy 2 12x 2y 3 Dy Chegg Com
71 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as wellBookmark Like 0 Dislike 0 ⚐ Report Your Answer Name * Email * (Required but will not be displayed) » Your answers will be displayedFirst let us bring equation into standard form in order to locate M(x, y), N(x, y) 2xy2 4 = 2(3 − x2y)dy dx (2xy2 4) dx 2(x2y − 3) dy = 0 First test whether it is exact DE ∂M ∂y = 4xy, ∂N ∂x = 4xy Now we can solve as exact DE ∫M(x, y) dx = x2y2 4x C1 ∫N(x, y) dy = − 6y x2y2 C2 DE has the solution




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation



Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community
In calculus, Leibniz's notation, named in honor of the 17thcentury German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively Consider y as a function of a variable x, or y = f(x)C y e x dx 2x cos y2 dy D Q x P y dA 0 1 x2 x 2 1 dydx 0 1 x x2 dx 2 3 x 3 2 1 3 x3 x 0 x 1 1 3 11 For C the circle x2 y2 4 (positively oriented), we have C y3 dx x3 dy D Q x P y dA D 3x2 3y2 dA 3 0 2 0 2 r3 drd 3 0 2 4d 24 We are asked to solve the differential equation (x − y) dy dx = x 2y We rearrange a little dy dx = x 2y x −y dy dx = 1 2(y x) 1 − (y x) (I) While I may not need to mention this, this differential equation is what is called a homogeneous differential equation I'll
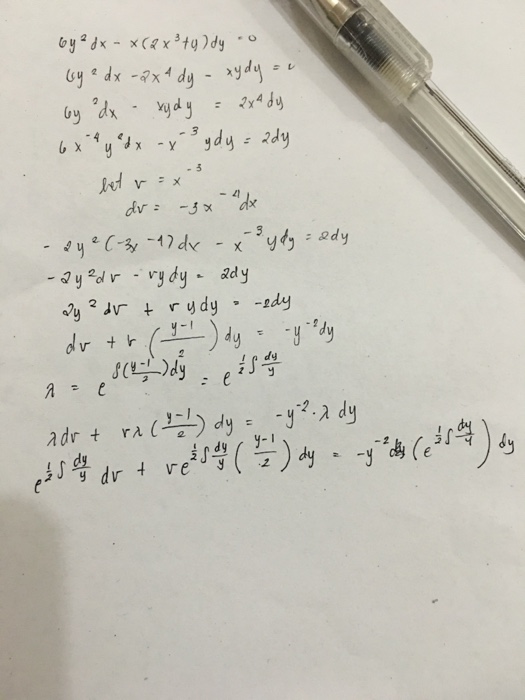



Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com



Solve Dy Dx X 2y 3 Xy 1 Sarthaks Econnect Largest Online Education Community
See Answer Check out a sample Q&A here Want to see this answer and more?Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!*Answer to 2 (x 2y 3) dx (2x 4y 3) dy = 0 3 (x y 2) dx (x y3) dy = 0 4 (x 2y 1) dx (x y 1) dy = 0;y(




Engineering Mathematics Notes




Solving Separable Differential Equations Calculus Socratic
Solve (xy2)dx (x2y3)dy=0 Maths Differential Equations Meritnationcom Hrithik Mishra, asked a question Subject Maths, asked on 14/7/18The solution of cosy (x siny 1) (dy / dx) = 0 The solution of dy / dx = 3 xy is The Solution Of Equations Cos 2 Theta Sin Theta 1 0 Lies The Solution Of Tan 2theta Tan Theta 1 Is The solution of the differential equation (dy / dx) y tan x = e x sec x is The solution of the differential equation (dy / dx) (y / x) = sin x isFree exact differential equations calculator solve exact differential equations stepbystep



Solved For Each Of The Following Obtain A Particular Solution Satisfying The Initial Condition Indicated 2y Dx 3x Dy When X 2 Y 3 2 Course Hero




Solve X Y 2 Dx X 2y 3 Dy 0 Maths Differential Equations Meritnation Com
An ordinary differential equation of first order and first degree can be written as dy dx = f(x,y) d y d x = f ( x, y) , where f(x,y) f ( x, y) is a function of two variables x,y x, y Which can # dy/dx=(x2y3)/(2xy3) # A Our standard toolkit for DE's cannot be used However we can perform a transformation to remove the constants from the linear numerator and denominator Consider the simultaneous equations # { ( x 2y 3 =0 ), (2x y 3=0) } => { ( x=1 ), (y=1) } # As a result we perform two linear transformationsCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps




Section 3 1 1 Implicitly Differentiate To Find Dy Dx Y3 X2 4 Slideshow And Powerpoint Viewer 2 Implicitly Differentiate To Find Dy Dx Y 4 X 3 2x 4y 3 Dy 3x 2 2 Dx Dy 4y




Lesson 6 Exact Equations Determine Whether Or Not Each Of
Learn how to solve differential equations problems step by step online Solve the differential equation xy*dx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac{1}{y}dy Integrate both sides of the5 Problem 15 (xy2 bx2y)dx(xy)x2 dy = 0 First, for this to be exact M y = 2xy bx2 = 3x2 2xy = N x So b = 3 With this, find the solution to the DE f(x,y) = Z M dx = Z xy 23x2ydx = 1 2 x y2 x3y g(y) And solve for g(y) f y = x 2y x3 g0(y) = x3 x y So we didn't need g(y) This leaves 1 2 x 2y x3y = C 6 Problem 18 Done inSolve dy/dx=2xy/(x^2y^2) check_circle Expert Answer Want to see the stepbystep answer?




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




التامة
1 dy 2y = 0 dx Definimos el factor integrante p (x) = 2 ´ factor integrante e 2dx = e2x multiplicamos la ecuacion por el factor integrante dy e2x dx 2e2x = 0 el lado izquierdo de la ecuacion se reduce a d 2x dx e y =0 separamos variables e integramos ´ d 2x ´ dx e y =0 dx c e2x y = c y = ce−2x 2 dy = 3y dx forma lineal dyX2ydx−(x3 y3)dy = 0 dydx = x2yx3 y3 Putting x = vydydx =v ydydv dydx = x2yx3 y3 ⇒ vydydv = v2y3v3y3 y3 = v2v3 1 ydydv = v2v3 1 −v = v2v3 1−v3 = v21 ⇒ v2dv = ydyY (0) = 1 is (A) x^3 = y^3 sin x Sarthaks eConnect Largest Online Education Community




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




Solve Linear Differential Equation 4x 2y 6 Dx X 3dy 0 Brainly In
Solve ( x 2 y − 2 x y 2) d x − ( x 3 − 3 x 2 y) d y = 0 written 34 years ago by smitapn612 ♦ 90 modified 15 months ago by sanketshingote ♦ 570 ADD COMMENT 1 Answer 1 658 views written 34 years ago by smitapn612 ♦ 90 modified 33 years ago by awariswati1 ♦ 770View this answer We are given x2 dy dx 2xy−y3 = 0 x 2 d y d x 2 x y − y 3 = 0 Rewrite {eq}\displaystyle \Rightarrow x^2 \ dy 2xy \ dx y^3 \ dy = See full answer below Solve the following differential equation (xy^2 2x)dx (x^2y 2y)dy = 0 asked May 12 in Differential Equations by Yajna ( 299k points) differential equations



Itligado Files Wordpress Com 14 06 Solution 4 Pdf




Solve X Y 1 Dx 2x 2y 3 Dy 0
Simple and best practice solution for (Xy^2x)dx(yx^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkY (xy^2 1)dx (2x (xy^2 1) 2y^4 )dy =0 Take xy^2 1 =V (x) then x = (V1)/y^2 , dx = dV/y^2 (2 (V1)/y^3)dy The equation becomes VdV/y 2y^4dy =0 Separating and integrating leads to (xy^2 1 )^2 = K (2/3)y^6 The solution is obtained in implicit form xy^2 = ( K (2/3)y^6 )^1/2Int (x^2 y^2 x y^3) dx dy, x=2 to 2, y=2 to 2 WolframAlpha Rocket science?




Vector Analysis By Alimkanwalimtinaa Issuu




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download
(x^3y^3)dx3xy^2dy=0 This deals with factoring binomials as the sum or difference of cubesSimple and best practice solution for (x2y)dx2(yx)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkUnlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard Examples



Www Tau Ac Il Levant Ode Solution 6 Pdf



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
Supposing that the correct equation is $$(x^2y^3y)dx(x^3y^2x)dy=0 \tag 3$$ one can find an integrating factor $$\mu(x,y)=\frac{x }{y^3}e^{x^2y^2}$$ Then an exact differential is obtained $$\frac{x }{y^3}e^{x^2y^2}\left((x^2y^3y)dx(x^3y^2x)dy\right)=0$$ $$e^{x^2y^2}\left((x^3\frac{x}{y^2})dx(\frac{x^4}{y}\frac{x^2}{y^3})dy\right)=0$$



Answered 5 X 4y 3 Dx X 6y 5 Dy Bartleby




X 2y Xy Y 0 Novocom Top




Doc Iii Exact Differentia Equation Joshua Pascual Academia Edu



3



Differential Equations Practice 38 2x 3 Xy 2 2y 3 Dx X 2y 2x Dy 0 Youtube




X Y 2 Dx 2x 2y 3 Dy 0 Brainly In




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com




Math 432 Hw 2 5 Solutions
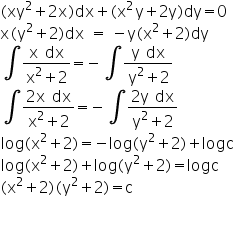



Xy 2 2x Dx X 2y 2y Dy 0 Mathematics Topperlearning Com X0ufmuww
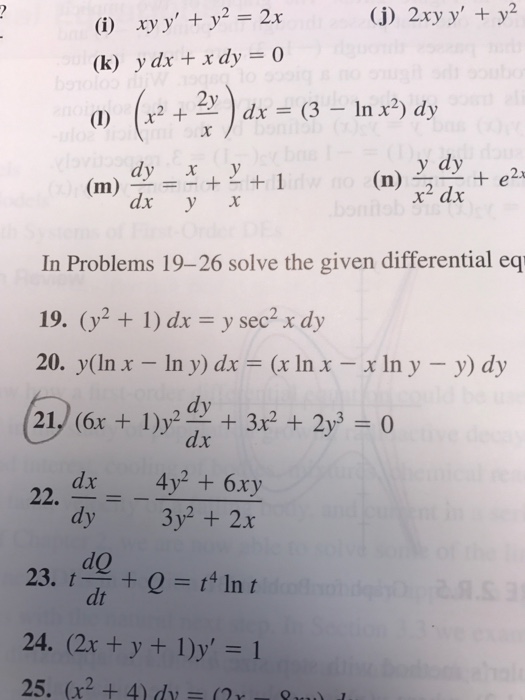



Xy Y Y 2 2x 2xy Y Y 2 Y Dx X Dy 0 X 2 Chegg Com
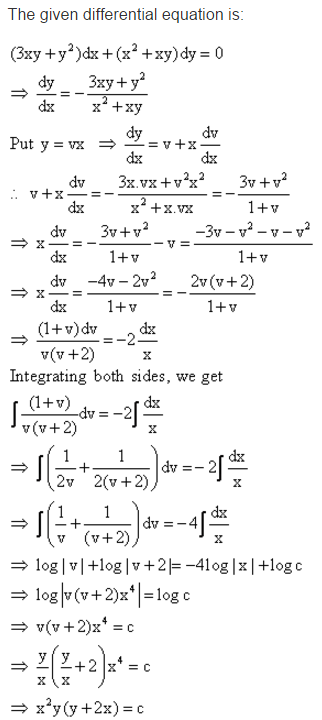



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633




Q21 Solve The Exact Different See How To Solve It At Qanda



What Is The Solution For Math Xy 2 2x 2y 3 Dx X 2y X 3y 2 Dy 0 Math Quora




Y 2 E Xy 2 4x 3 Dx 2xye Xy 2 3y 2 Dy 0 Brainly In



Www Ualberta Ca Rjia Math215 Hwks Sol7 Pdf




Dy Dx X Y 1 2x 2y 3 Youtube



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora
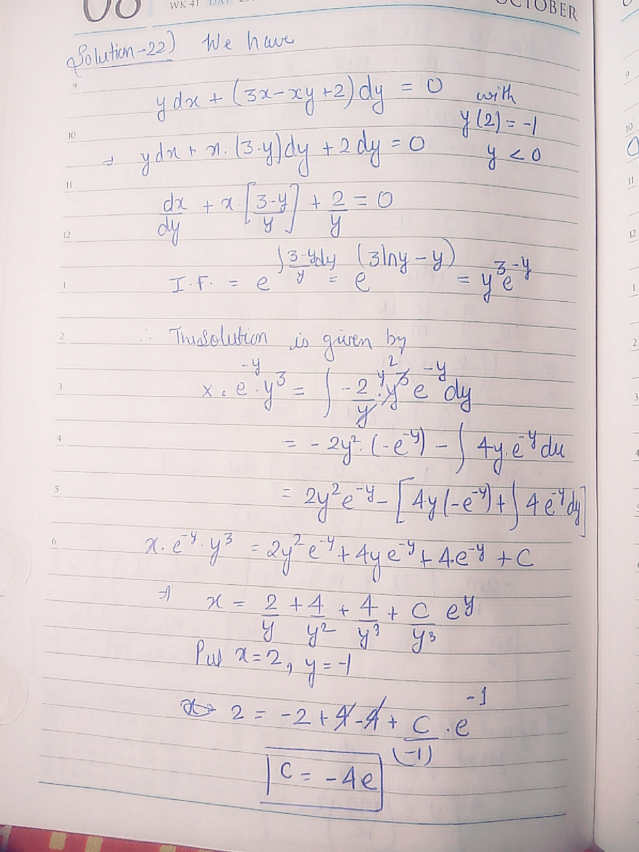



Solve The Initial Value Problem Y Dx 3x Xy 2 Dy 0 Y 2 1 Y 0 Homework Help And Answers Slader



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



2 X Y 3 X 2 Y 3 Zonealarm Results




In Determine Whether The Given Differential Equation Chegg Com




Consider The Equation X3 Y3 Dx Xy 2 Dy 0 Express This Equation In The Form Dy Dx F X Y G X Y And Solve The Equation Maths Differential Equations Meritnation Com




Suggested Problems Engr213 Studocu



1



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf




Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is




Help With Number 4 5 Differential Equations The Answers Are Provided But Can Not Determine Homeworklib




Y X Dx Y 3 Ln X Dy 0 Novocom Top




Engineering Mathematics Notes




Evaluate The Line Integral By Two Methods Directly C Xy Dx X 2 Dy C Is The Rectangle With Vertices 0 0 3 0 3 1 And 0 1 Homework Help And Answers Slader




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download
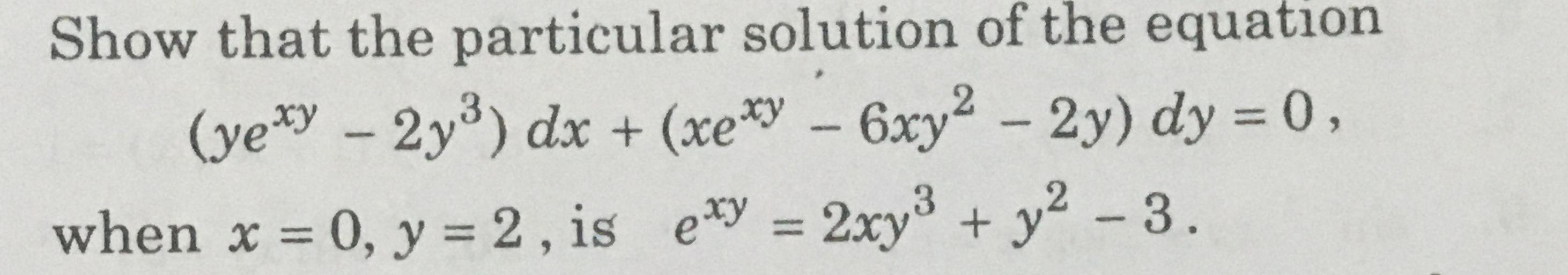



Show That The Particular Solution Of The Equation Yexy Math




Review Problems In Problems 1 30 Solve The Equation Chegg Com




Chapter 04 2500 Solved Problems In Differential Equations Docsity




Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection




Solve The Following Differential Equations I Y 2 D X Left X Y X 2 Right D Y 0 Ii X 2 Y D X Left X 3 Y 3 Right D Y 0 Iii Frac D Y D X Tan Left Frac Y X Right Frac Y X Iii Frac D Y D X Frac X 2 Y 2 X Y 0 Iv




Example 21 Find General Solution Ydx X 2y2 Dy 0




Solve Dy Dx 2x Y 1 X 2y 3 Youtube
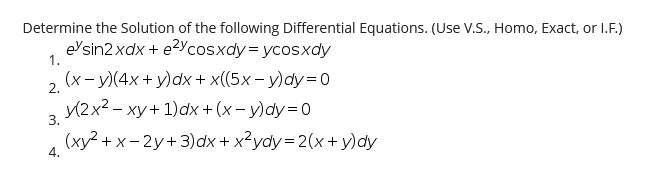



Answered Determine The Solution Of The Following Bartleby




For Problems 26 Determine An Integrating Factor Chegg Com



Find Dy Dx X 3 X 2 Y Xy 2 Y 3 81 Edurev Class 12 Question




Solve X 3 2y 3 Dx 3xy 2dy 0



Http 1 160 97 198 8080 Xmlui Bitstream Handle 2 2 chapter 1 11 Pdf Sequence 2




Engineering Mathematics Notes




X Y 2 Dx X 2y 3 Dy 0 Brainly In




Ercise 11 C Eind The Solutio See How To Solve It At Qanda




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



Http Pages Mtu Edu Struther Courses Old Other Older 3521 10 Quizstuff Fromgil Ch 2 Pdf
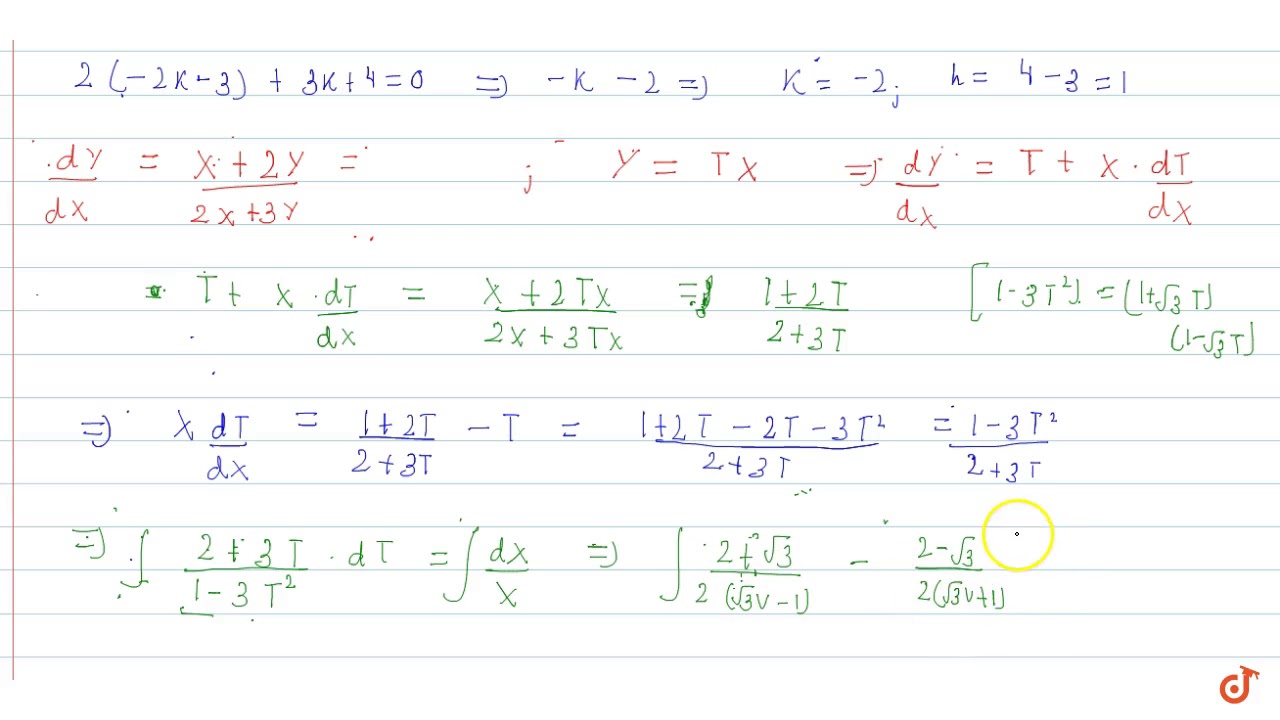



Solve Dy Dx X 2y 3 2x 3y 4 Youtube



Can You Solve 1 X 3 Dy Dx X 2y Quora




For What Value Of N Is Following A Homogeneous Differential Equation




4 1 Implicit Differentiation



Find The General Solution Of X 2y3 Dy Dx Y Studyrankersonline




Engineering Mathematics Notes



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community




Solve X Y 2 Dx X 2y 3 Dy 0 Maths Differential Equations Meritnation Com




Math 432 Hw 2 4 Solutions




X 2y 3 Dx X 3y 2 Dy 0 Novocom Top




3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange




Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora



Solved Test Exactness And Solve Question 1 2xy 3x 2 Dx X 2 2y Dy 0 Question 2 Cosx Xsinx Y 2 Dx 2xydy 0 Question 3 2xydx X 2 Course Hero




1st Order Ode Problem Set
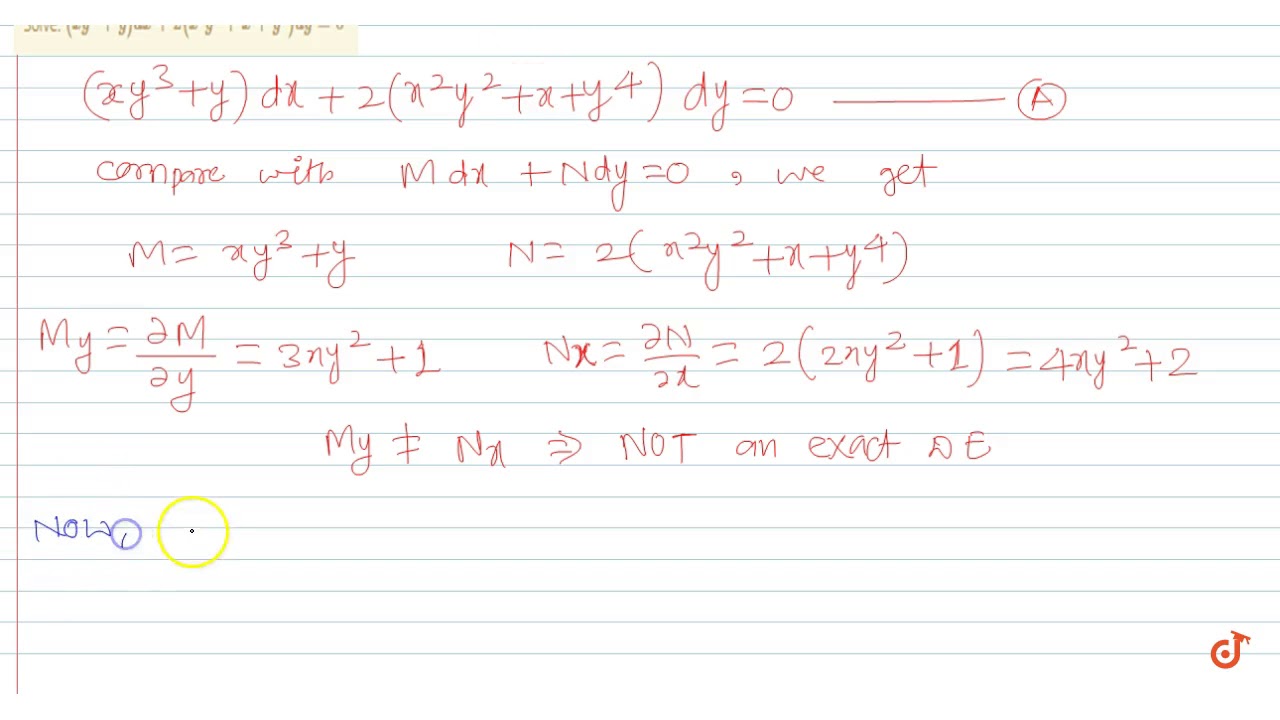



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



1



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora




Solve X Y 2 Dx X 2y 3 Dy 0 Maths Differential Equations Meritnation Com




Exact Differential Equations




X 2 Xy 4 Dx 2y 3dy 0 Mathematics Stack Exchange




Answered 3 3x Xy 2 Dx X 2y Dy 0 Bartleby




X 3 X Y 4 Dx 2y 3dy 0




What Is The Solution Of X Y 2 Dx X 2y 3 Dy 0




Chapter 04




Solve The Differential Equation X Y 2 X Dx Y X 2 Y Dy 0



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf



Http Fractal Math Unr Edu Ejolson 285 15 Extraprob Pdf




Exact Equations Example 3 Video Khan Academy



0 件のコメント:
コメントを投稿